Diziler
Diziler
Aynı veri türünden birbiriyle ilişkili verilerin bir arada tutulmasını sağlayan yapılara dizi denir. Dizinin içerisinde yer alan her bir ayrı veriye eleman denilmektedir. Bu elemanlara indis numaraları verilir ve bu numaralar üzerinden yerlerine ulaşılır.
Dizileri tek boyutlu ve çok boyutlu diziler şeklinde sınıflandırabiliriz.
Tüm programlama dillerinde olduğu gibi Java dilinde de dizi (array) yapısı son derecede önemli bir veri yapısıdır. Dizi yapısını kısaca tanımlarsak:
Dizi, bilgisayar belleğinde aynı isim altında genellikle aynı tipten çok sayıda veriyi bir arada saklayan veri yapısıdır. Aşağıda, x adlı bir dizinin mantıksal görünümü verilmiştir:
| 4 | 2 | 7 | 22 | 11 | 3 |
| 0 | 1 | 2 | 3 | 4 | 5 |
Dizinin bir adı ve dizi içerisindeki elemanın dizinin kaçıncı elemanı olduğunu belirten bir indisi (subscript, index) vardır. Örneğin, yukarıdaki x adlı dizi için x ifadesi bu dizinin 3 numaralı elemanını yani 22 değerini göstermektedir. Dizinin indisi Java dilinde daima köşeli parantez ile belirlenir:
Java dilinde bir dizinin ilk elemanının indisi daima 0’dır; son elemanın indisi ise diziye ayrılan yer sayısının 1 eksiğine eşittir. Yukardaki x dizisinin 6 elemanı vardır; ilk elemanının indisi 0 ve son elemanının indisi de 5’tir. Java Programı içinde Dizinin Bildirilmesi Bir Java programı içinde diziyi tanıtmak için, new sözcüğünü kullanarak belirli bir tipten yeni bir nesne tanımlama yolu izlenir. Dizinin tipi, adı ve maksimum eleman sayısı bir bildiri deyimi içinde belirtilir:
Tip DiziAdı[ ] = new Tip [ Eleman Sayısı ];
veya eşdeğeri
Tip [ ] DiziAdı = new Tip [ Eleman Sayısı ];
Örneğin, yukarıdaki x dizisi için,
int [ ] x= new int [6] ;
şeklinde bildirimde bulunulacaktır. x dizisi 6 elemanlıdır ve elemanları int türündedir.
Dizi için ne gereklidir?
Dizi yapısına, aynı türden bir veri grubunu tümüyle bellekte saklı tutmanın gerekli olduğu uygulamalarda ihtiyaç duyarız. Örneğin, verilerin sıralanması, bir veri grubuna ait bazı istatistiksel bilgilerin hesaplanması (standart sapma vb.) gibi uygulamalar bu tür uygulamalardandır.
Örnek: Aşağıda aynı işlemi gerçekleştiren iki farklı Java programı verilmiştir. Her iki program da, bilgisayara girilen 5 adet sayının toplamını bulmaktadır.
Dizi kullanmayan sürüm
import java.util.Scanner;
public class Dizi1{
public static void main(String[] args)
{ Scanner giris = new Scanner(System.in);
int girilenSayi, toplam, i ;
toplam = 0; girilenSayi = 0;
for (i = 1; i <= 5; i++)
{
System.out.print("Bir sayi giriniz: ");
girilenSayi = giris.nextInt();
toplam = toplam + girilenSayi;
}
System.out.println(i-1+ " tane sayi girdiniz.");
System.out.println("Toplami " +toplam+ " ediyor.");
}
}
Bu programın şöyle bir çıktısı olacak:
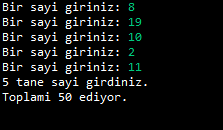
NOT: Scanner sınıfı bir akıştan (Stream) gelen veriyi bir değişkene atamak için kullanılmıştır. System.in akışı, kullanıcının konsola veri girmesi için kullanılır.
Dizi kullanan sürüm
import java.util.Scanner;
public class Dizi2{
public static void main(String[] args)
{
Scanner giris = new Scanner(System.in);
int sayi[] = new int[6];
int toplam, i; toplam = 0;
for (i = 1; i <= 5; i++)
{
System.out.print("Bir sayi giriniz: ");
sayi[i] = giris.nextInt(); t
oplam = toplam + sayi[i];
}
System.out.println("Girdiniz sayilarin toplami: " + toplam);
System.out.println("Sayi dizisinin ikinci elemani: " + sayi[2]);
}
}
Bu programın çıktısı şöyle olacak:

Örnekte, dizi kullanmayan sürümde, bilgi giriş ortamından girilecek
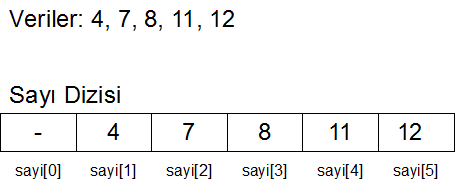
olan sayılar (sırasıyla 4, 7, 8, 11, 2 sayıları) toplanacak ve sonuç=32 olarak bulunacak ve yazdırılacaktır.
Aslında, ikinci sürümde de aynı veriler girildiği takdirde, sonuçta gene t = 32 şeklinde bu sayıların toplamı yazdırılacaktır.
Bu iki program arasında çok önemli bir fark mevcuttur: dizi kullanmayan sürümde, girilen her sayı, girilenSayi adlı değişkende saklanacak ve her seferinde o andaki girilenSayi değişkeninin değeri o ana kadar olan sayılar toplamını saklayan toplam değişkenine eklenecektir. Her yeni sayı girildiğinde, girilenSayi değişkeninde saklı bulunan bir önceki sayı değeri silinecektir. Bu durumda programın sonunda girilenSayi değişkeninde en son girilen değer olan 2 değeri saklanacaktır.
System.out.println(girilenSayi+ " tane sayi girdiniz.");
deyimi ile yazdırılan sayı da bu olacaktır.
Dizi kullanmayan sürümde, örneğin program sonunda ”Girdiğimiz 3. sayı neydi?” diye merak eder ve bunu yazdırmak istersek bunun olanaksız olduğunu görürüz. Oysa ikinci sürümde dizi kullanıldığı için her sayı, sayi dizisinin bir elemanı olarak sonuna kadar bellekte saklanır. Bu noktada program sonunda,
System.out.println("Sayi dizisinin ikinci elemani: " + sayi[2]);
deyimiyle 3. sayıyı yazdırmamız mümkündür.
Dizilere Başlangıç Değeri Atanması
Birçok bilgisayar dilinde olduğu gibi, Java dilinde de dizilere dizinin tanımlanması esnasında başlangıç değeri atanması mümkündür. Örneğin,
intx ={3,-2,1,4,11};
şeklindeki bildiri deyimi ile, x dizisine aşağıdaki gibi değerler atanmıştır: Örnek: Başlangıç Değeri Atanması
public class Dizi3
{
public static void main(String[] args)
{
int [] sayi={2,1,5,3,6};
double toplam = 0; int i;
for(i=0; i<=4; i++)
{
toplam=toplam+sayi[i];
}
System.out.println("Toplam: "+toplam);
}
}
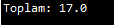
Burada çıktımız şu şekilde gerçekleşecek:
Dizi tanımında diğer bir yöntem
Dizi boyutunu bir değişken olarak tanımladıktan sonra diziyi tanımlarken bu değişkeni kullanmamız da mümkündür. Aşağıdaki komutlarla 5 elemanlı bir dizi tanımlayabiliyor fakat diziye ilk değer ataması yapamıyoruz:
int DIZI_BOYUT=5;
int [] sayi;
sayi=new int[DIZI_BOYUT];
Örnek: Dizi Boyutunun Bir Değişkenle Belirtilmesi
import java.util.Scanner;
public class Dizi4{
public static void main(String[] args)
{
Scanner giris = new Scanner(System.in);
int DIZI_BOYUT = 5; int[] sayi;
sayi = new int[DIZI_BOYUT];
int toplam=0; int i;
for (i = 0; i <= 4; i++) {
System.out.print(i + ". dizi elemanini giriniz: ");
sayi[i] = giris.nextInt(); toplam = toplam + sayi[i];
}
System.out.println("Toplam: " + toplam);
}
}
Programın çıktısı:

Bir fonksiyon parametresi olarak diziler
Fonksiyonlar ve fonksiyon parametreleri konusunda bir fikrimiz olduğuna göre hemen şunu söyleyebiliriz: Bir dizi, bir fonksiyon parametresi olarak kullanılabilir. Çağıran fonksiyon ya da program, dizi türündeki bu parametreye yine dizi türünde olmak üzere bir argüman geçirebilir. Bir dizi, bir fonksiyon parametresi olacaksa; dizinin tipi, adı ve içi boş olan köşeli parantezler fonksiyonun parametre listesinde görünmelidir. Örneğin,
static int topla_dizi(int[] x, int n)
gibi bir fonksiyon başlığında x tam sayı tipinde bir dizidir. n parametresi ise dizinin eleman sayısıdır. Bu fonksiyonu çağıran fonksiyon veya program içinde, a dizisi,
int[ ]a={2,8,3,7,5};
şeklinde tanımlanmışsa, yukardaki topla_dizi adlı fonksiyon,
toplam=topla_dizi(a,5);
şeklinde çağrılabilir.
Örnek: "n" Elemanlı Bir "x" Dizisinin Toplamını Bulan Bir Fonksiyon ve Çağıran Programla Birlikte Kullanılması
public class Dizi5 {
public static void main(String[] args){
int[] a={2,8,3,7,5};
int toplam;
toplam=topla_dizi(a,5);
System.out.println("Toplam: "+toplam);
}
static int topla_dizi(int [] x,int n){
int i, ictoplam;
ictoplam=0;
for(i=0; i<n; i++) {
ictoplam+=x[i];
}
return ictoplam;
}
}
Bu kodun çıktısı:

Çok Boyutlu Diziler
Çok boyutlu diziler içinde en yaygın kullanım alanı iki boyutlu diziler için söz konusudur.
Elimizde aşağıdaki gibi bir veri mevcut olsun:
1998 Yılı Otomobil Satışları
(Not: Tablodaki rakamlar gerçek değildir, örnek amaçlı verilmiştir.)
| MARKA | OCAK | ŞUBAT | MART |
|---|---|---|---|
| Fiat | 700 | 600 | 650 |
| Renault | 900 | 800 | 700 |
| VW | 300 | 400 | 350 |
| Opel | 500 | 450 | 470 |
| Ford | 600 | 500 | 480 |
Bu tabloda, 1998 yılında çeşitli otomobil markaları için gerçekleştirilen ilk üç aylık satışları görüyoruz. Bu tür bir bilgiyi bilgisayara yükleyerek aşağıdaki sorulara cevap olabilecek işlemleri tablo üzerinde gerçekleştirmek isteyebiliriz:
- Her marka için 3 aylık satış toplamı nedir? (Tablodaki satır toplamları)
- Her ay için tüm markaların satış toplamları nelerdir? (Tabloda sütun toplamlarının hesaplanması)
- Her marka için en çok satışın gerçekleştirildiği ay hangisidir? (Satırlardaki en büyük elemanların tespiti)
- Her ay için en çok satışın gerçekleştirildiği marka hangisidir? (Sütunlardaki en büyük elemanların tespiti)
- Tüm marka ve tüm aylar için otomobil satışları toplamı nedir? (Tablonun genel toplamının bulunması)
Tablodaki bilgileri Java dilinde, bilgisayar belleğinde iki boyutlu dizi (two dimensional array) yapısı adı verilen yapı içinde saklayabiliriz. Matematikteki matris yapılarının Java'daki doğal karşılığı da bu tip iki boyutlu dizi yapısıdır.
Yukarıdaki tablo içinde, sayısal olmayan bilgileri ve başlıkları ihmal ederek sadece satışlardan oluşan sayısal bilgiyi dikkate alırsak ve bu bilgiyi satis adlı bir tabloda saklarsak, aşağıdaki yapıyı elde ederiz:
satis
| 700 | 600 | 650 |
| 900 | 800 | 700 |
| 300 | 400 | 350 |
| 500 | 450 | 470 |
| 600 | 500 | 480 |
Java'da, 5 satır ve 3 sütundan oluşan bu tabloyu aşağıdaki şekilde tanımlayabiliriz:
int satis=new int [5,3];
Burada satis adlı iki boyutlu dizinin bir elemanına referans vermek için program içinde, şeklinde bir ifade kullanırız. Burada satis dizinin adı, i satır indisi ve j de sütun indisidir.Satis dizisinin satır indisleri 0'dan başlar ve 4'e kadar devam eder. Sütun indisleri ise, 0 ile 2 arasında değerler alır. Aşağıda, satis dizisinin bellekte Java tarafından saklanan biçimini görüyoruz:
Buna göre, satis[0,0] elemanı 700, satis[2,1] elemanı 400 ve satis[4,2] elemanı ise 480’dir.
Satis adlı iki boyutlu dizinin eleman sayısı ise 5x3=15’tir.
İki boyutlu dizinin elemanlarını okutmak
İki boyutlu dizinin elemanlarını Java programının çalıştırılması sırasında klavyeden girmek için aşağıdaki gibi bir program kullanabiliriz. Aşağıdaki örnek programda 3 satır ve 2 sütunu olan satis adlı tablonun elemanları klavyeden giriliyor ve daha sonra tablo ekrana aktarılıyor. Şimdi bu örnek programı inceleyelim:
import java.util.Scanner;
public class CokBoyutluDizi1 {
public static void main(String[] args){
Scanner giris = new Scanner(System.in);
int[][] satisTablosu = new int[3][2];
int i, j;
/* kullanıcıdan satış tablosu
* bilgilerini alalım */
System.out.print("Satis [0,0]=");
satisTablosu[0][0] = giris.nextInt();
System.out.print("Satis [0,1]=");
satisTablosu[0][1] = giris.nextInt();
System.out.print("Satis [1,0]=");
satisTablosu[1][0] = giris.nextInt();
System.out.print("Satis [1,1]=");
satisTablosu[1][1] = giris.nextInt();
System.out.print("Satis [2,0]=");
satisTablosu[2][0] = giris.nextInt();
System.out.print("Satis [2,1]=");
satisTablosu[2][1] = giris.nextInt();
/* bellekteki satis tablosu
* elemanlarının ekrana yazdırılması */
System.out.println("Satis tablonuz");
for (i = 0; i <= 2; i++) {
for (j = 0; j <= 1; j++) {
System.out.print(satisTablosu[i][j] + " ");
}
System.out.println();
}
}
}
İki boyutlu dizi elemanlarına ilk değer atanması
İki boyutlu dizinin elemanları sabit olacaksa yani program her çalıştırıldığında değerleri değişmiyorsa, bu durumda iki boyutlu dizi elemanlarına programın içinde ilk değer ataması yapabiliriz
İlk değer ataması, iki boyutlu dizi değişebilecek olsa bile, dizi üzerinde gerçekleştirilecek tekrarlı bazı işlemler için de bir başlangıç değeri oluşturmak için gerekli olabilir. satisTablosu adlı dizinin elemanlarını kod bloku içinde ilk değer ataması yoluyla aşağıdaki gibi oluşturabiliriz:
int[][] satisTablosu = new int[][]{
{700,600,650},
{900,800,700},
{300,400,350},
{500,450,470},
{600,500,480}
};
public class CokBoyutluDizi2 {
public static void main(String[] args){
int [][]satisTablosu = new int[][]{
{700,600,650},
{900,800,700},
{300,400,350},
{500,450,470},
{600,500,480}};
int i,j;
/*bellekteki satis tablosu
* elemanlarının ekrana yazdırılması*/
System.out.println("Satis tablosu");
for(i=0; i<=4; i++){
for(j=0; j<=2; j++) {
System.out.print(satisTablosu[i][j]+" " );
}
System.out.println();
}
}
}
length fonksiyonunun kullanılması
length fonksiyonu ile iki boyutlu dizinin her bir boyutundaki eleman sayısını bulmamız mümkün.

satisTablosu adlı dizi yukardaki gibi tanımlanmışsa satisTablosu.length ifadesi 0. boyuta ait eleman sayısını yani satır sayısını (5), satisTablosu
.length ifadesiyse 1. boyuta ait eleman sayısını yani sütun sayısını (3) verecektir. Aşağıdaki Java kodu, bu fonksiyonların nasıl kullanılabileceğini gösteriyor:
public class CokBoyutluDizi3 {
public static void main(String[] args){
int [][]satisTablosu = new int[][]{
{700,600,650},
{900,800,700},
{300,400,350},
{500,450,470},
{600,500,480}
};
int i,j;
/*bellekteki satis tablosu
* elemanlarının ekrana yazdırılması*/
System.out.println("Satis tablosu");
/*
* döngülerin sınırlarını length()
* fonksiyonlarıyla belirliyoruz
* */
for(i=0; i<satisTablosu.length; i++) {
for(j=0; j<satisTablosu[0].length; j++) {
System.out.print(satisTablosu[i][j]+" " );
}
System.out.println();
}
}
}
Program çıktısı:

ÖRNEK: Satış Tablosunun Satır ve Sütun Toplamlarının ve Tablodaki Elemanların Genel Toplamının Bulunması
public class CokBoyutluDizi4 {
public static void main(String[] args){
int [][]satisTablosu = new int[][]{
{700,600,650},
{900,800,700},
{300,400,350},
{500,450,470},
{600,500,480}
};
int i, j, toplamSatis, toplamOtomobilSayisi=0;
/*bellekteki satisTablosu dizisinin
* elemanlarının ekrana yazdırılması*/
System.out.println("Otomobil satislari tablosu");
for(i=0; i<satisTablosu.length; i++) {
for(j=0; j<satisTablosu[0].length; j++) {
System.out.print(satisTablosu[i][j]+" " );
}
System.out.println();
}
/*
* Her marka için 3 aylık satış toplamlarını
* yani dizinin satır toplamlarını yazdıralım
* */
for(i=0; i<=4; i++) {
toplamSatis=0;
for(j=0; j<=2; j++)
toplamSatis=toplamSatis+satisTablosu[i][j];
System.out.println(i+1+". markanin toplam satisi: "+toplamSatis);
}
/*
* Her ay için 5 markanın satış toplamlarını
* yani tablodaki sütunların toplamlarını
* gösterelim
* */
System.out.println();
toplamOtomobilSayisi=0;
for(j=0; j<=2; j++){
toplamSatis=0;
for(i=0; i<=4; i++)
{
toplamSatis=toplamSatis+satisTablosu[i][j];
toplamOtomobilSayisi=toplamOtomobilSayisi+satisTablosu[i][j];}
System.out.println(j+1+". ayda 5 marka icin toplam satis miktari: "+toplamSatis);
}
/*3 AY ICIN TOPLAM OTOMOBIL SATISI-GENEL TOPLAM*/
System.out.println("3 aylik toplam otomobil satisi"+toplamOtomobilSayisi);
}
}
Program çıktısı
ÖRNEK: Aşağıda verilen matrisi, bilgisayarda otomatik olarak oluşturacak bir Java programı yazalım.
2!
|
4!
|
6!
|
8!
|
10!
|
12!
|
14!
|
16!
|
18!
|
public class CokBoyutluDizi5 {
public static void main(String[] args){
double[][] dizi=new double[3][3];
int i,j,sayimiz;
sayimiz=2;
for(i=0; i<=2; i++) {
for(j=0; j<=2; j++) {
dizi[i][j]=faktoriyel(sayimiz);
System.out.println(sayimiz+"!="+dizi[i][j]);
sayimiz=sayimiz+2;
}
}
}
static double faktoriyel(int n){
double fakt;
int i;
fakt=1.0;
for(i=1; i<=n; i++) {
fakt=fakt*i;
}
return fakt;
}
}
Programın çıktısı şöyle olacaktır:

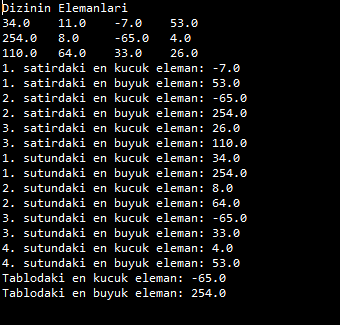
ÖRNEK: Önceden belirleyeceğimiz 3'e 4'lük bir tabloda yer alan elemanların en küçük ve en büyük değerdeki elemanı bulan bir Java programı yazalım. Ayrıca bu program her satırdaki ve sütundaki en küçük ve en büyük elemanları da bulabilsin.
public class CokBoyutluDizi6 {
public static void main(String[] args){
double[][] tablo=new double [][]{
{34,11,-7,53},
{254,8,-65,4},
{110,64,33,26}
};
int i,j;
double kucukEleman, buyukEleman, enKucuk, enBuyuk;
/*tablonun yazdırılması*/
System.out.println("Dizinin Elemanlari");
for(i=0; i<=2; i++) {
for (j=0; j<=3; j++) {
System.out.print(tablo[i][j]+"\t");
}
System.out.println();
}
/* Her satırdaki en büyük ve en küçük
* elemanların bulunması*/
for(i=0; i<=2; i++) {
kucukEleman=3.4e38;
buyukEleman=-3.4e38;
for(j=0; j<=3; j++) {
if(tablo[i][j]<kucukEleman) {
kucukEleman=tablo[i][j];
}
if(tablo[i][j]>buyukEleman) {
buyukEleman=tablo[i][j];
}
}
System.out.println((i+1)+". satirdaki en kucuk eleman: "+kucukEleman);
System.out.println((i+1)+". satirdaki en buyuk eleman: "+buyukEleman);
}
/* Her sütundaki en büyük ve en küçük
* elemanın bulunması*/
/* Ek olarak tablodaki en büyük ve en küçük
* elemanın bulunması */
enKucuk=3.4e38;
enBuyuk=-3.4e38;
for(j=0; j<=3; j++) {
kucukEleman=3.4e38;
buyukEleman=-3.4e38;
for (i=0; i<=2; i++) {
if(tablo[i][j]<kucukEleman) {
kucukEleman=tablo[i][j];
}
if(tablo[i][j]>buyukEleman) {
buyukEleman=tablo[i][j];
}
if(tablo[i][j]<enKucuk) {
enKucuk=tablo[i][j];
}
if(tablo[i][j]>enBuyuk) {
enBuyuk=tablo[i][j];
}
}
System.out.println((j+1)+". sutundaki en kucuk eleman: "+kucukEleman);
System.out.println((j+1)+". sutundaki en buyuk eleman: "+buyukEleman);
}
System.out.println("Tablodaki en kucuk eleman: "+enKucuk);
System.out.println("Tablodaki en buyuk eleman: "+enBuyuk);
}
}
Programın çıktısı:
ÖRNEK: Matris Çarpımı
Aşağıdaki Java programı,
Cmn = Amk Bkn
şeklindeki matris çarpımı işlemini gerçekleştiriyor:
public class CokBoyutluDizi7 {
public static void main(String[] args){
int[][] aMatris=new int [][]{{2,1},{-1,4},{5,3}};
int[][] bMatris=new int [][]{{3,2,1,-1},{4,-2,1,2}};
int[][] cMatris=new int [3][4];
int i,j,k,t;
/*a ve b matrislerinin yazdırılması*/
System.out.println("A matrisi");
for(i=0; i<=2; i++) {
for(j=0; j<=1; j++) {
System.out.print(aMatris[i][j]+"\t");
}
System.out.println();
}
System.out.println("B matrisi");
for(i=0; i<=1; i++){
for(j=0;j<=3;j++) {
System.out.print(bMatris[i][j]+"\t");
}
System.out.println();
}
/* a ve matrisinin çarpımı olan
* c martisinin hesaplanması */
for(k=0; k<=3; k++) {
for(i=0; i<=2; i++) {
cMatris[i][k]=0;
for(j=0; j<=1; j++) {
cMatris[i][k]=cMatris[i][k]+
aMatris[i][j]*bMatris[j][k];
}
}
}
System.out.println("C matrisi");
for(i=0; i<=2; i++)
{
for(j=0;j<=3;j++)
System.out.print(cMatris[i][j]+"\t");
System.out.println();
}
}
}
Programın çıktısı:
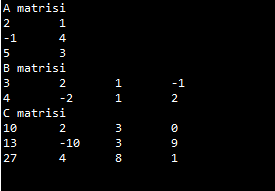
ÖRNEK: Aşağıdaki matrisi otomatik olarak oluşturan ve yazdıran bir Java programı geliştirelim.
| ( 2! - 1 ) / 3 | ( 4! + 2 ) / 5 | ( 6! - 3 ) / 7 |
| ( 8! + 4 ) / 9 | ( 10! - 5 ) / 11 |
( 12! + 6 ) / 13
|
public class CokBoyutluDizi8 {
public static void main(String[] arg){
double matris[][]=new double[2][3];
int i,j,p,u;
int k;
char isaret;
p=-1;
k=2;
u=1;
for(i=0; i<=1; i++) {
for(j=0; j<=2; j++) {
matris[i][j]=(faktoriyel(k)+p*u)/(k+1.0);
if(p<0) {
isaret='-';
}
else {
isaret='+';
}
System.out.println("["
+i+
"]["
+j+
"] = ("
+k+
"!"
+isaret+u+
") / "
+(k+1)+
" = "
+matris[i][j]+
"\t");
k=k+2;
p=-p;
u++;
}
}
}
public static double faktoriyel(double sayi){
double fakt=1.0;
int i;
for(i=1; i<=sayi; i++) {
fakt=fakt*i;
}
return fakt;
}
}
Programın çıktısı şu şekilde olacaktır:
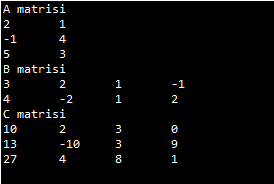
ÖRNEK: Aşağıdaki matrisin en büyük elemanının bulunduğu sütunda yer alan en küçük elemanı bulan bir Java programı geliştirelim.
| 56 | 23 | 678 | 231 |
| 234 | 21 | 78 | 23 |
| 654 | 33 | 22 | 67 |
| 189 | 35 | 56 | 89 |
Yazılacak olan Java programı doğru çalıştığı takdirde, tablodaki en büyük elemanı 678 olan sütuna gelip oradaki en küçük sayı olan 22'yi bulmalıdır.
public class CokBoyutluDizi9 {
public static void main(String[] arg){
double[][] matris={
{56,23,678,231},
{234,21,78,23},
{654,33,22,67},
{189,35,56,89}
};
int i,j,k;
k=0;
double enBuyuk,enKucuk;
enBuyuk=matris[0][0];
for(i=0; i<=3; i++){
for(j=0; j<=3; j++){
if(matris[i][j]>enBuyuk)
{
enBuyuk=matris[i][j];
k=j;
}
System.out.print("["+i+"]["+j+"]=" + matris[i][j]+"\t");
}
System.out.println();
}
enKucuk=matris[0][k];
for(i=0; i<=3; i++) {
if(matris[i][k]<enKucuk) {
enKucuk=matris[i][k];
}
}
System.out.println("En buyuk elemanin bulundugu sutundaki en kucuk sayi"+enKucuk);
}
}
Programın çıktısını aşağıda bulabilirsiniz:
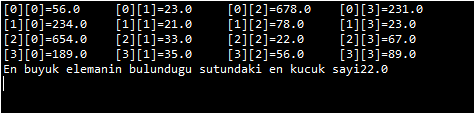
ÖRNEK: Aşağıdaki matrisin içindeki en küçük ikinci elemanı bulan bir Java programı geliştirelim.
| 56 | 23 | 678 | 231 |
| 234 | 21 | 78 | 26 |
| 654 | 33 | 32 | 67 |
| 189 | 35 | 56 | 89 |
Program, bu tablo içindeki en küçük ikinci eleman olan 23’ü bulmalıdır.
public class CokBoyutluDizi10 {
public static void main(String[] arg){
double[][] matris={
{56,23,678,231},
{234,21,78,26},
{654,33,32,67},
{189,35,56,89}
};
int i,j,y,x;
y=0;
x=0;
double enKucuk;
enKucuk=matris[0][0];
for(i=0; i<=3; i++) {
for(j=0; j<=3; j++){
if(matris[i][j]<enKucuk) {
enKucuk=matris[i][j];
x=i;
y=j;
}
System.out.println("["+i+"]["+j+"] = "+matris[i][j]+"\t");
}
}
matris[x][y]=100000000000.0;
enKucuk=matris[0][0];
System.out.println("");
for(i=0; i<=3; i++){
for(j=0; j<=3; j++){
if(matris[i][j]<enKucuk)
{
enKucuk=matris[i][j];
y=j;
x=i;
}
System.out.print("["+i+"]["+j+"]=" + matris[i][j]+" ");
}
System.out.println("");
}
System.out.println("");
System.out.println("");
System.out.println("Matristeki ikinci en kucuk eleman: "+enKucuk);
System.out.println("Bu elemanin satir ve sutunu "+x+"'a "+y);
}
}
Programın çıktısı:
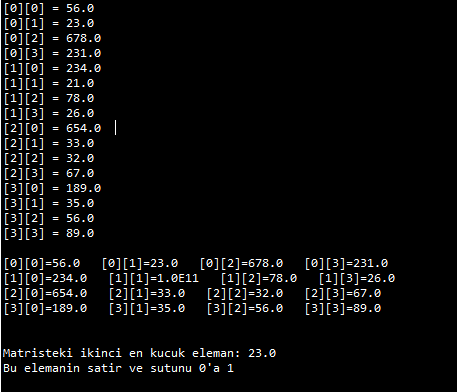
ÖRNEK: Aşağıdaki matrisin içindeki tek sayıları tek boyutlu bir diziye yükleyen ve bu diziyi sıralayan bir Java programı geliştirelim.
| 56 | 23 | 678 | 231 |
| >234 | 21 | 78 | 26 |
| 654 | 33 | 32 | 67 |
| 189 | 35 | 56 | 89 |
Tablodaki tek sayılar koyu hale getirilmiştir. Yazılacak program bu sayıları tek boyutlu diziye yükleyerek sıralamalıdır.
public class CokBoyutluDizi11 {
public static void main(String[] arg){
int[][] matris={
{56,23,678,231},
{234,21,78,26},
{654,33,32,67},
{189,35,56,89}
};
int i,j,k;
k=0;
int temp=0;
int[] tekSayilar=new int[16];
/*tek sayıları bulalım*/
for(i=0; i<=3; i++) {
for(j=0; j<=3; j++) {
if (matris[i][j]/2*2 != matris[i][j]) {
tekSayilar[k]=matris[i][j];
k++;
}
System.out.print("["+i+"]["+j+"]=" + matris[i][j]+"\t");
}
System.out.println();
}
System.out.println();
System.out.println("Tek sayilardan olusan dizi:");
for(i=0; i<=k-1; i++) {
System.out.print(tekSayilar[i]+"\t");
}
System.out.println();
System.out.println();
/*tek sayılardan oluşan diziyi küçükten
* büyüğe olacak şekilde sıralayalım*/
for(i=0; i<tekSayilar.length; i++) {
for(j=0; j<tekSayilar.length; j++) {
if(tekSayilar[i]>tekSayilar[j]) {
temp=tekSayilar[i];
tekSayilar[i]=tekSayilar[j];
tekSayilar[j]=temp;
}
}
}
System.out.println("Tek sayilardan olusan dizinin siralanmis hali:");
for(i=k-1; i>=0; i--) {
System.out.print(tekSayilar[i]+"\t");
}
}
}
Programın çıktısı:
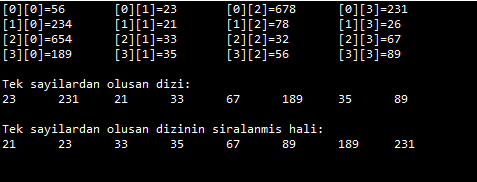
ÖRNEK: Alfabetik karakterlerden oluşan aşağıdaki matris veriliyor:
| m | a | v | b |
| z | y | c | e |
| g | f | p | q |
| r | h | i | k |
Bu matristeki c-r arasındaki harfleri tek boyutlu bir diziye yerleştirerek bu diziyi sıralayan bir Java programı geliştirelim.
public class CokBoyutluDizi12 {
public static void main(String[] arg){
char[][] matris={
{'m','a','v','b'},
{'z','y','c','e'},
{'g','f','p','q'},
{'r','h','i','k'}
};
int i,j,k;
k=0;
char temp;
char[] harfler=new char[16];
/*dizideki harflerden c-r arasınd
* olanları bulalım */
for(i=0; i<=3; i++){
for(j=0; j<=3; j++) {
if(matris[i][j]>='c' && matris[i][j]<='r') {
harfler[k]=matris[i][j];
k++;
}
System.out.print("["+i+"]["+j+"]=" + matris[i][j]+"\t");
}
System.out.println();
}
/*c-r arası harfleri ekrana basalım*/
System.out.println();
System.out.println("c-r arasi harfler: ");
for(i=0; i<=k-1; i++) {
System.out.print(harfler[i]+" ");
}
/*c-r arasındaki harfleri sıralayalım*/
for(i=0; i<harfler.length; i++){
for(j=0; j<harfler.length; j++){
if(harfler[i]>harfler[j]) {
temp=harfler[i];
harfler[i]=harfler[j];
harfler[j]=temp;
}
}
}
System.out.println();
System.out.println("Siralanmis halleri: ");
/*sıralanan harfleri ekrana basalım*/
for(i=k-1; i>=0; i--) {
System.out.print(harfler[i]+" ");
}
}
}
Programın çıktısı:
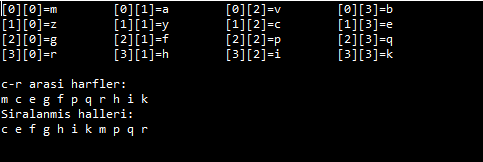
Android uygulamalarında, özellikle uzaktaki bir kaynaktan ya da veri tabanından çoklu veri çektiğinizde dizi yapılarını kullanıyor olacağız.
Yorumlar
Yorum Gönder