Verilerin Sıralanması - Sıralama (Sortıng) Algoritmaları

Tüm dünyada belirli bir zaman periyodu içinde bilgisayarların en çok hangi işlemi yaptıkları sorulsa bu sorunun cevabı mutlaka sıralama olurdu. Gerçekten de sıralama işlemi en çok ihtiyaç duyulan işlemdir; çünkü biz veri ya da veri gruplarını incelerken bunların belirli bir alana göre sıralanmış olmasını isteriz.

Verilerin sıralanmış olması, başka bazı işlemler için de ön koşul oluşturur. Bu işlemlerden ilk akla geleni ikili arama işlemidir (binary search). İkili arama işlemi sadece sıralanmış veriler üzerinde uygulanabilir. Sıralama konusu bilgisayar biliminde üzerinde çok araştırma yapılmış bir konu olduğu için bu konuda bilinen pek çok algoritma mevcuttur.

Sıralama işlemi, hem sayısal hem de string (karakter zinciri) türündeki veriler için söz konusudur.

Her iki türdeki veriler için de iki tür sıralama yapılabilir:

Artan (Ascending) yani küçükten büyüğe doğru.
Azalan (Descending) yani büyükten küçüğe doğru.

Sıralamalara örnekler:

2,24,748,790,1456

listesi sayısal veri içermektedir ve artan şekilde sıralıdır.

1789,545,12,-55

listesi sayısal veri içermektedir ve azalan biçimde sıralıdır.

A,ALI,AYSE,BERIL,MITHAT,ZEYNEP

Listesi string türü veri içermektedir ve artan sırada sıralanmıştır.

ZEYNEP,MERT,BERTAN,AHMET

Listesi ise string türü veri içermektedir ve azalan biçimde sıralanmıştır.

Bilgisayar String Türü Verileri Karşılaştırabilir Mi?

Bilgisayar string türü verileri de büyüklük-küçüklük açısından karşılaştırabilir. Bilgisayar bu işlemi yaparken karşılaştırdığı stringler içindeki karakterlerin sayısal ASCII kodlarını almakta ve gerçekte bunları karşılaştırmaktadır.

Örneğin, 'B' < 'A' şeklindeki karşılaştırma gerçekte bilgisayar belleğinde 66<65 şeklinde bir sayısal karşılaştırmaya dönüştürülmektedir; çünkü A'nın sayısal ASCII kodu 65 ve B'nin sayısal ASCII kodu ise 66'dır.

Karşılaştırılan iki string içinde önce ilk karakterler karşılaştırılır; bunlar eşitse, bir sonraki karakterlere geçilir.

İlk n adet karakterleri eşit olan iki string'ten biri n+1 karakterli diğeri n karakterli ise, bu durumda uzun olan (yani n+1 karakterli olan) büyük kabul edilir.

Örnek karşılaştırmalar:

'AHMET'> 'BERİL'

Sonuç doğrudur.

'BERTAN' ='bertan'

Sonuç yanlıştır. ASCII tablosunda küçük harflere ait sayısal kodlar, büyük harflerinkinden daha büyüktür.

'CEM'>'C'

Sonuç doğrudur.

Yer Değiştirme Sıralaması (Exchange Sort)

Anlaşılması en kolay olan sıralama yöntemlerinden biridir. Sıralamayı n elemanlı bir L listesi içinde yapacağımızı ve artan sıralama olacağını var sayıyoruz.

En başta veri listesinin ilk sırasındaki eleman ikinci ile karşılaştırılır. Sıralama artan türde sıralama ise ve L1>L2 ise, L1 ve L2 arasında yer değiştirme işlemi yapılır. Daha sonra L1 ile L3 karşılaştırılır ve gene artan sıralama yapılıyorsa ve L1>L3 ise, L1 ve L3 arasında yer değiştirme yapılır. Bu karşılaştırmalar ilk geçişte L1-L4, L1-L5 ve nihayet L1-Ln arasında yapılır. Birinci geçişin sonunda veri listesi içindeki en küçük veri en başa gelir.

İkinci geçiş ise, L2 ve L3'ün kaşılaştırmasıyla başlar ve L2>L3 ise yer değiştirme olur. Sonra L2-L4, L2-L5 ve nihayet L2-Ln karşılaştırmaları yapılır. İkinci geçişin sonunda ise veri içindeki en küçükten bir sonraki veri listenin ikinci yerine yerleşir.

Üçüncü geçişte L3-L4, L3-L5 ve nihayet L3-Ln karşılaştırmalarıyla listenin 3. yerine doğru eleman yerleştirilir.

Son geçiş n-1'nci geçiştir ve bu geçişte sadece Ln-1 ile Ln liste elemanları karşılaştırılır ve gerekiyorsa yer değiştirme yapılır.

n-1'nci geçiş sonunda liste sıralanmıştır.

Yer değiştirme algoritmasına örnek:

Yer değiştirme sıralaması yöntemini daha iyi anlayabilmek için algoritmayı örnek bir veri üzerinde çalıştıralım. Örnek veri aşağıdaki gibi olsun:

1. Geçiş (Pass)

45 ile 21 karşılaştırılır ve yer değiştirme yapılır:

21 ile 3 karşılaştırılır ve yer değiştirme yapılır:

3 ile 16 karşılaştırılır; yer değiştirme olmaz.

3 ile 8 karşılaştırılır; yer değiştirme olmaz.

1. geçiş sonunda L listesi

şeklindedir ve listedeki en küçük eleman en başa gelmiştir.

2. Geçiş

2. geçiş, 45 ile 21'in karşılaştırmasıyla başlar ve yer değiştirme olur.

3. Geçiş

4. Geçiş

45 ile 21 karşılaştırılır ve yer değiştirme olur:

Görüldüğü gibi 4. geçiş (n=5 ve n-1=4) sonunda veri sıralanmıştır.

İki elemanın yer değiştirmesi işlemi

Li ve Lj liste elemanları belli bir anda tek bir değer saklayabilirler. Bilgisayar belleğinde de durum böyle olacaktır; yani Li ve Lj ye birer bellek konumu ayrılacak ve burada birer değer saklanacaktır. Bir bellek konumuna yeni bir değer atanınca önceki değer silinecektir. Bir başka deyişle, Li nin değeri Lj'ye atansa, Lj'nin değeri silinecektir. Halbuki yer değiştirme yapabilmek için Lj'nin değerini de Li'ye atamamız gerekir. Bu durumda yardımcı bir alana ya da bellek alanına ihtiyacımız olacaktır. Bu yardımcı alana T diyelim. Buna göre yer değiştirme şu şekilde olacaktır:

Önce Li nin değeri T'ye aktarılır:
Sonra Lj nin değeri Li'ye aktarılır:

Yer değiştirme sıralaması ile ilişkili program

<html>

<head>

<TITLE>İÇİNDEKİLER</TITLE>

</head>

function SIRALAEXC( a )

{

var i, j, t;

i = 0;

while( i < (a.length- 1) ) {

j = i + 1;

while( j < a.length) {

if( a[i] > a[j] ) {

t= a[i];

a[i] = a[j];

a[j] = t;

}

j++;

}

i++;

}

var dizi =[ 10, 23, 8, 253, 191, 711, 2, 27, 1, 813];

document.write("<H3>"+"SIRALAMA ISLEMINDEN ONCEKI DIZI"+"</H3>");

document.write("<H3>"+dizi.join(" ")+"</H3>");

SIRALAEXC( dizi);

document.write("<H3>"+"SIRALAMA ISLEMINDEN SONRAKİ DIZI"+"</H3>");

document.write("<H3>"+dizi.join(" ")+"</H3>");

</SCRIPT>

</body>

</html>

Kabarcık Sıralama (Bubble Sort) Yöntemi

Anlaşılması kolay bir sıralama yöntemi de bubble sort (kabarcık sıralama) adı verilen yöntemdir. n elemanlı L listesini artan sırada sıralamak istediğimizi varsayalım.

Kabarcık sıralama yönteminde yer değiştirme sıralaması yönteminden farklı olarak, her geçişte listenin komşu olan elemanları birbiri ile karşılaştırılır ve ilk geçişte liste içindeki en büyük eleman en sona gider. Bundan sonraki geçiş ilk n-1 eleman arasında gerçekleştirilir ve bu geçişin sonunda da en büyük eleman n-1'nci konuma yerleşir. Benzer şekilde bir sonraki geçiş arta kalan n-2 eleman arasında gerçekleştirilir ve bu geçişte de bu en son liste parçası içindeki en büyük eleman n-2'nci yere yerleşir.

Bu işlemler benzer şekilde sürer. Herhangi bir geçişte hiçbir yer değiştirme olmamışsa liste sıralanmış demektir.

Kabarcık sıralama: örnek veri üzerinde adımlar

Şimdi n=5 elemanı olan L listesi aşağıdaki gibi verilmiş olsun:

1. Geçiş

Bu aşama 1. geçişin sonudur ve yukarıda da belirtildiği gibi 1. geçişin sonunda veri içindeki en büyük eleman en sona yerleşmiştir.

2. Geçiş

2. geçiş, 1. geçişin bıraktığı noktadaki liste ile başlar.

2. geçiş sona ermiş ve bu geçişte, ilk 4 elemanın en büyüğü olan 56 sondan bir önceki yere yani doğru yerine yerleşmiştir. 3. geçiş ilk 3 eleman arasında olacaktır.

3. Geçiş

L1 ile L2 mukayese edilir; 12<34 olduğu için bu iki eleman yer değiştirmez.

L2 ile L3 mukayese edilir; 34<11 olduğu için bu iki eleman yer değiştirir:

3. geçişin sonudur ve veri içindeki 3. en büyük eleman sondan 3. yere yerleşmiştir.

4. Geçiş

L1 ile L2 mukayese edilir; 12>11 olduğu için bu iki eleman yer değiştirir:

4. geçiş sona ermiştir ve verinin sıralandığı görülmektedir.

Kabarcık sıralaması (bubble sort) algoritması

Veri listesi üzerinde birbirini izleyen geçişleri uygula.
Her geçiş esnasında birbirini izleyen iki liste elemanı arasında karşılaştırma işlemi yap ve gerekiyorsa yer değiştirme işlemini gerçekleştir.
Bir geçiş esnasında hiçbir yer değiştirme olmuyorsa ya da n-1 geçiş tamamlanmışsa (veri miktarının n olduğu var sayımı ile) sıralama işlemini sona erdir.

Kabarcık sıralama algoritmasında bir geçişi daha formel olarak şu şekilde ifade edebiliriz:

i=1,2,... n-1 şeklinde değişirken

Şayet Li >Li+1 ise, Li ile Li+1 ‘e yer değiştir

Kabarcık sıralama algoritmasının performansı da O(n2) mertebesindedir. Veri miktarı arttıkça sıralama için gerekli zaman veri miktarının karesi ile orantılı olarak artar.

Örnek: Kabarcık sıralama JavaScript uygulaması

<html>

<head>

<title> İÇİNDEKİLER </title>

</head>

var a=[34,5,11,9,76,43,77,789,51,10];

var i;

var t,f;

document.write("<h3>"+"SIRALAMADAN ONCEKI DIZI"+"</h3>");

document.write("<h3>"+a.join(" ")+"</h3>");

f=0;

while(f==0){f=1;

for(i=0;i<=a.length-1;i++)

{if(a[i]>a[i+1])

{t=a[i];

a[i]=a[i+1];

a[i+1]=t;

f=0;

}}}

document.write("<h3>"+"SIRALAMA ISLEMINDEN SONRAKİ DIZI"+"</h3>");

document.write("<h3>"+a.join(" ")+"</h3>");

</script>

</body>

</html>

Hızlı Sıralama (Quicksort) Algoritması

Genel olarak kabarcık sıralama yer değiştirme sıralaması ve seçme sıralaması yöntemlerinden daha etkin bir sıralama algoritmasıdır ve hızlı sıralama (quicksort) adıyla bilinir. Quicksort algoritması sıralanacak diziyi iki parçaya ayırır ve bu parçalama işlemi alt parçalar için de sürdürülür. Bu özelliğiyle quicksort algoritması özyineli (rekürsif, ing: recursive) nitelikteki bir algoritmadır.

Algoritmanın ilerleyişi

Sıralanacak olan dizi a1,a2,…..an dizisi olsun. Bu liste içinden bir elemanı seçelim (bu seçme işlemi çeşitli şekillerde gerçekleştirilebilir; en basiti ilk elemanı seçmek şeklinde olabilir). Liste içinden seçtiğimiz elemana pivot eleman ya da ayırıcı eleman (separator) adı verilir. Bu elemanı p ile gösterelim. a dizisinin p'den küçük olan elemanları bir sol alt liste içine (bu listeye L adını verelim) ve p'den büyük olan elemanları da bir sağ alt liste içine yerleşecektir. Bu sağ alt listeye de R adını verelim. Bu durumda a listesi,

a⇒ L , p , R

şeklinde 3 parçadan oluşmuş bir biçime dönüştürülür.

L içindeki tüm elemanlar p'den daha küçük ya da ona eşittir. R içindeki tüm elemanlar ise p'den büyüktür. p ise dizi içinde doğru yere yerleşmiştir.

Algoritmanın ifadesi

qsort(x,b,s) {x dizisi sıralanacaktır. Bu dizi xb,xb+1,..xs şeklindedir} begin if s > b begin { sıralanacak eleman mevcuttur} P pivot elemanını liste içinden seç(mesela ilk eleman olabilir) ve

x dizisini aşağıdaki biçimde parçala! Xb,...xk , p, xk+1,...xb qsort(x,b,k) qsort(x,k+2,b) end end

Yöntemi bir örnek dizi üzerinde açıklayalım. Sıralanacak dizi aşağıdaki gibi olsun:

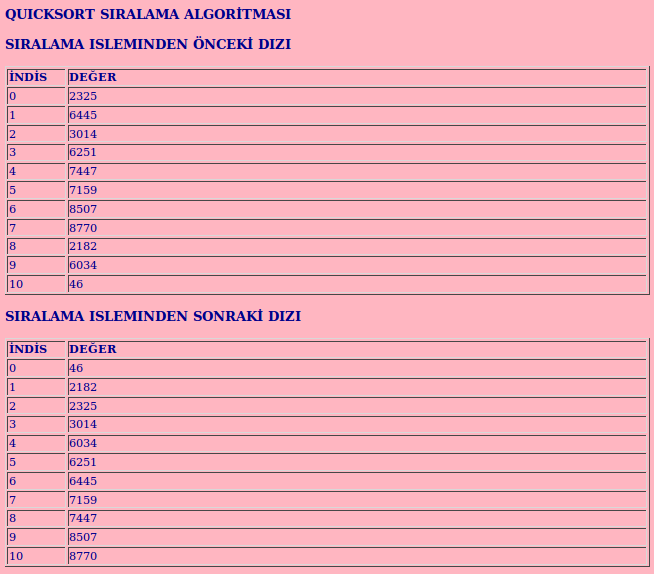
Hızlı sıralama algoritması için geliştirilen JavaScript programının listesi

<html>

<head>

<TITLE>İÇİNDEKİLER</TITLE>

</head>

var a=new Array(11);

document.write("<H3>"+"QUICKSORT SIRALAMA ALGORİTMASI"+"</H3>");

document.write("<H3>"+"SIRALAMA ISLEMINDEN ÖNCEKİ DIZI"+"</H3>");

document.writeln( "<TABLE BORDER = '2' WIDTH = '50%'>" );

document.writeln( "<TR><TD WIDTH = '80'><B>İNDİS</B>"

+ "<TD><B>DEĞER</B></TR>" );

for ( i = 0; i < a.length; i++ )

{

a[i]=Math.floor(1+Math.random()*10000);

document.writeln( "<TR><TD>" + i + "<TD>" +

a[ i ] + "</TR>" );

}

document.writeln( "</TABLE>" );

HIZLI_SIRALA(a, 0, a.length-1);

document.write("<H3>"+"SIRALAMA ISLEMINDEN SONRAKİ DIZI"+"</H3>");

document.writeln( "<TABLE BORDER = '2' WIDTH = '50%'>" );

document.writeln( "<TR><TD WIDTH = '80'><B>İNDİS</B>"

+ "<TD><B>DEĞER</B></TR>" );

for ( i = 0; i < a.length; i++ )

{

document.writeln( "<TR><TD>" + i + "<TD>" +

a[ i ] + "</TR>" );

}

document.writeln( "</TABLE>" );

/* HIZLI_SIRALA adlı fonksiyon 3 argüman alıyor

İlk argüman sıralanacak elemanları içeren a dizisidir.

İkinci argüman dizinin başlangıç pozisyonunu ve 3. argüman ise dizinin son elemanını gösteriyor

HIZLI_SIRALA fonksiyonunun her çağrılışında dizinin farklı bir parçası işlem görecektir.*/

function HIZLI_SIRALA( a, sol, sag)

{var dur, son,u;

if (sol >= sag)

return;

u=Math.floor((sol+sag)/2);

DEGIS(a, sol, u);

/*Dizinin ortasındaki eleman pivot olarak alınıyor ve listenin en soluna kaydırılıyor. */

son = sol;

for (dur = sol + 1; dur <= sag; dur++)

if (a[dur] < a[sol])

DEGIS(a, ++son, dur);

DEGIS(a, sol, son);

HIZLI_SIRALA(a, sol, son-1);

HIZLI_SIRALA(a, son+1, sag);

}

/* DEGIS fonksiyonu dizi içindeki iki elemanın yerlerini değiştirmektedir.*/

function DEGIS(a, i, j)

{var t;

t = a[i];

a[i] = a[j];

a[j] = t;

}

</SCRIPT>

</body>

</html>

Bu Blogda Ara

Öznur Kına Yazılım Notları